1. Key Generation

Create an RSA key pair by carrying out the actions listed below:
  • - pick two large prime numbers, p and q.
  • - Calculate n = p * q, the modulus.
  • - Compute the Euler totient function, which is given by n = (p - 1) * (q - 1).
  • - Select an integer e such that gcd(e, ɸ(n)) = 1 and 1< e < ɸ(n). The public is going to be the public totient.
  • - Use the multiplicative inverse of e modulo (n) to compute the private exponent, d.
  • - (e, n) is the private key, while (d, n) is the public key.
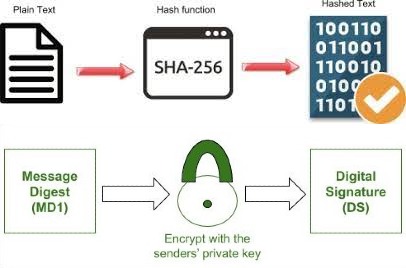
2. SHA-256

SHA-256, which stands for Secure Hash Algorithm 256-bit, is a cryptographic hash function that belongs to the SHA-2 family. It is widely used for secure data integrity checks, digital signatures, and password storage.The main purpose of a cryptographic hash function like SHA-256 is to take an input, such as a message or a file, and produce a fixed-size output, which is a 256-bit (32-byte) hash value. This hash value is unique to the input data, meaning even a small change in the input will produce a significantly different output.

3. Signing

  • 1. Compute the hash value of the document by a hash function (SHA-256).
  • 2. Apply a padding method to the hash value to ensure its length matches the length of the RSA modulus.
  • 3. Encrypt the padded hash value using the private key exponent, d, and the modulus, n. This produces the digital signature.
4. Verification

Steps To Verify


  • 1. Obtain the digital signature and the public key (e, n) of the signer.
  • 2. Decrypt the digital signature using the public key:
  • public key = (signature)^e mod n.
  • 3. Remove the padding from the decrypted signature, which will yield the hash value.
  • 4. calculate the hash value of the received document using the same hash function.
  • 5. Compare the recalculated hash value with the decrypted hash value. If they match, the document has not been tampered, and the digital signature stands valid.