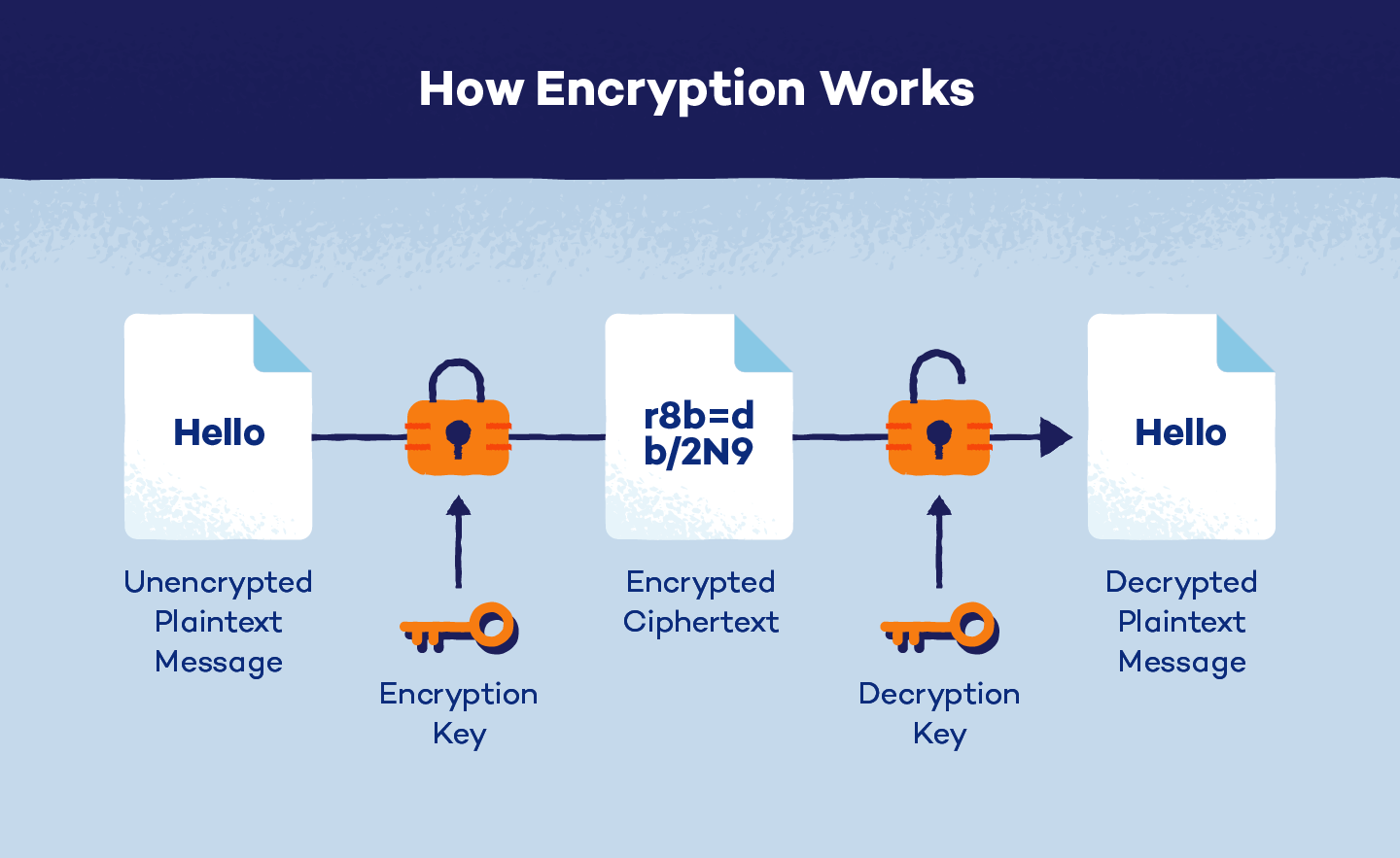
RSA
RSA (Rivest-Shamir-Adleman) is a widely used cryptographic algorithm that enables secure communication and data encryption. It was first introduced in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman. RSA is based on the mathematical properties of prime numbers and modular arithmetic.